第二章传输线理论

微波的频率范围:3GHz~300GHz

传输线方程（电报方程）

$\begin{cases} \frac{dV(z)}{dz}=-Z\cdot I(z) \\ \\ \frac{dI(z)}{\partial z}=-Y\cdot V(z) & \end{cases}$

特性阻抗

$Z_{0}=\frac{R+j\omega L}{\gamma}=\sqrt{\frac{R+j\omega L}{G+j\omega C}}=\frac{V_{0}^{+}}{I_{0}^{+}} =-\frac{V_{0}^{-}}{I_{0}^{-}}$

入射波和反射波

$v(z,t)=|V_{0}^{+}|\cos(\omega t-\beta z+\Phi^{+})e^{-\alpha z}+|V_{0}^{-}|\cos(\omega t+\beta z+\Phi^{-})e^{\alpha z}=V_{0}^{+}e^{-\gamma z}+V_{0}^{-}e^{\gamma z}$

$\mathrm{i}(z,t)=\frac{|v_{0}^{+}|}{z_{0}}\cos(\omega t-\beta z+\Phi^{+})e^{-\alpha z}-\frac{|v_{0}^{+}|}{z_{0}}\cos(\omega t+\beta z+\Phi^{-})e^{\alpha z}=\mathrm{I} _{0}^{+}e^{-\gamma z}-I_{0}^{-}e^{\gamma z}$

传输线上任一点处的电压和电流均由两部分组成，第一部分表示由信号源向负载方向传播的行波，称之为入射波，第二部分表示由负载向信号源方向传播的行波，称之为反射波

入射波的振幅随传播方向距离z的增加按指数规律衰减，相位随z的增加而滞后；反射波的振幅随距离z的增加而增加，相位随z的增加而超前

复传播常数

$\gamma=\alpha+j\beta=\sqrt{Z\cdot Y}=\sqrt{(R+j\omega L)\cdot(G+j\omega C)}$

衰减常数 $\alpha$

相移常数 $\displaystyle{\beta=\frac{2\pi}{\lambda}}$

对于低耗传输线, $R<<\omega L,G<<\omega C$

$\begin{aligned} & \gamma=j\omega\sqrt{LC}\cdot\sqrt{(1+\frac{R}{j\omega L})(1+\frac{G}{j\omega C})}\approx j\omega\sqrt{LC}+(\frac{R}{2}\sqrt{\frac{C}{L}}+\frac{G}{2}\sqrt{\frac{L}{C}}) \end{aligned}$

$\alpha=\alpha_{\mathrm{c}}+\alpha_{d}=\frac{R}{2}\sqrt{\frac{C}{L}}+\frac{G}{2}\sqrt{\frac{L}{C}}$

$\beta=\omega\sqrt{L\cdot C}$

衰减常数是由传输线的导体电阻损耗 $\alpha_c$ 和填充介质的漏电损耗 $\alpha_d$ 两部分组成

相速 $\displaystyle\upsilon_{p}=\frac{dz}{dt}=\frac{\omega}{\beta}=\lambda\cdot f$

相波长 $\displaystyle\lambda_{p}=v_{p}T=\frac{v_{p}}{f}=\frac{2\pi}{\beta}$

无耗传播线(R=0,G=0)

$\alpha=0,\beta=\omega\cdot\sqrt{L\cdot C}$

特性阻抗 $\displaystyle Z_{0}=\sqrt{\frac{L}{C}}$

无耗传输线的特征阻抗是实数

相速 $\displaystyle\upsilon_{p}=\frac{1}{\sqrt{LC}}$

双导线和同轴线上行波的相速 $\displaystyle\upsilon_{p}=\frac{1}{\sqrt{\mu\cdot\varepsilon}}=\frac{\upsilon_{0}}{\sqrt{\varepsilon_{r}}}$

双导体传输线和同轴线上行波电压和电流的相速等于周围介质中的光速，与频率无关，只决定于周围介质的相对介电常数，这种波为非色散波

相波长 $\displaystyle\lambda_{\mathrm{p}}=\upsilon_{p}T=\frac{\upsilon_{p}}{f}=\frac{2\pi}{\beta}=\frac{\lambda_{0}}{\sqrt{\varepsilon_{r}}}$

输入阻抗 $Z_{in}$

$Z_{in}(z)=Z_{0}\frac{Z_{L}-jZ_{0}\tan(\beta z)}{Z_{0}-jZ_{L}\tan(\beta z)}$

$Z_{in}(l)=Z_{0}\frac{Z_{L}+jZ_{0}\tan(\beta l)}{Z_{0}+jZ_{L}\tan(\beta l)}$

无耗传输线上任意相距 $\lambda/2$ 处的阻抗相同, 具有 $\lambda/2$ 重复性

$Z_{in}(l)=Z_{L}\quad l=n\frac{\lambda}{2}\quad(n=0,1,2,...)$

传输线上距离负载 $\lambda/4$ 奇数倍的各点的输入阻抗等于特性阻抗的平方和负载阻抗之比

$Z_{in}(l)=\frac{Z_{0}^{2}}{Z_{L}}\quad l=(2n+1)\frac{\lambda}{4} \quad(n=0,1,2,...)$

输入导纳

$Y_{in}(z)=Y_0\frac{Y_L-jY_0\tan(\beta z)}{Y_0-jY_L\tan(\beta z)}$

(电压)反射系数:距终端z处的反射波电压Vr(z)与入射波电压Vi(z)之比

$\Gamma_{\nu}(z)=\frac{V_{r}(z)}{V_{i}(z)}=\frac{V_{o}^{-}}{V_{o}^{+}}e^{j2\beta z}$

终端反射系数 $\Gamma_L$

$\Gamma_L=\frac{V_0^-}{V_0^+}=\left|\Gamma_L\right|e^{j\Phi_L}$

传输线上任意一点的反射系数

$\Gamma(z)=\Gamma_Le^{j2\beta z}=\left|\Gamma_L\right|e^{j(\Phi_L+2\beta z)}=\left|\Gamma_L\right|e^{j\Phi}$

对均匀无耗传输线来说, 任意点反射系数 $\Gamma(z)$ 大小均相等, 沿线只有相位按周期变化, 其周期为 $\lambda/2$ , 即反射系数也具有 $\lambda/2$ 重复性

$\Gamma(z)=\frac{Z_{in}(z)-Z_0}{Z_{in}(z)+Z_0}$

当 $Z_L=Z_0$ 时, $\Gamma_L=0$ , 即负载终端无反射, 此时传输线上反射系数处处为零, 称之为负载匹配

传输线上的电压电流可以用反射系数和入射波表示

$V(z)=V_{i}(z)[1+\Gamma(z)]$

$I(z)=I_i(z)[1-\Gamma(z)]$

电压驻波比（VSWR）

$\rho=\frac{\left|V\right|_{\max}}{\left|V\right|_{\min}}$

驻波比与反射系数的关系

$\rho=\frac{\begin{vmatrix} V \end{vmatrix}_{\max}}{\begin{vmatrix} V \end{vmatrix}_{\min}}=\frac{1+ \begin{vmatrix} \Gamma \end{vmatrix}}{1- \begin{vmatrix} \Gamma \end{vmatrix}}$

$\left|\Gamma\right|=\frac{\rho-1}{\rho+1}$

行波系数K

$K=\frac{\left|V\right|_{\min}}{\left|V\right|_{\max}}=\frac{1-\left|\Gamma\right|}{1+\left|\Gamma\right|} =\frac{1}{\rho}$

回波损耗（RL）

$RL=-20\lg\lvert\Gamma\rvert dB$

当源与传输线匹配时，微波信号源的资用功率为 $\displaystyle P_{a}=\frac{\left|E_{g}\right|^{2}}{8Z_{0}}$

当传输线终端不匹配时

$P(z)=\frac{1}{2}\operatorname{Re}\left\{V(z)\cdot I^{*}(z)\right\}=\frac{1}{2}\operatorname{Re} \left\{\frac{\left|V_{i}(z)\right|^{2}}{Z_{0}}[1-\left|\Gamma(z)\right|^{2}+\Gamma (z)-\Gamma^{*}(z)]\right\}$

对于无耗传输线

$P(z)=\frac{1}{2}\frac{\left|V_{i}(z)\right|^{2}}{Z_{0}}[1-\left|\Gamma(z)\right| ^{2}]=P_{i}(z)-P_{r}(z)=\text{入射波功率}-\text{反射波功率}$

无耗传输线上通过任意点的传输功率等于该点的入射波功率与反射波功率之差．对于均匀无耗传输线，通过线上任意点的传输功率都是相同的

一般在电压波腹点(最大值点)或电压波节点(最小值点)处计算传输功率，即 $\displaystyle P(z)=\frac{1}{2}|V_{\max}|\cdot|I_{\min}|=\frac{1}{2}\cdot\frac{|V_{\max}|^{2}}{Z_{0}} \cdot K$

$|V_{max}|$ 由传输线线间击穿电压 $V_{br}$ 决定,在不发生击穿情况下，传输线允许传输的最大功率称为传输线的功率容量,即 $\displaystyle P_{br}=\frac{1}{2}\cdot\frac{\left|V_{\mathrm{br}}\right|^{2}}{Z_{0}}\cdot K$

传输线的功率容量与行波系数K有关。K愈大，功率容量 $P_{br}$ 也愈大。在驻波状态下传输线传输的功率为零

均匀无耗传输线的特殊情况:

行波状态（阻抗匹配，无反射波）
$\left|\Gamma\right|=0,\rho=1,K=1,RL=\infty$
输入阻抗 $Z_{\mathrm{in}}(z){=}Z_{0}$
驻波状态（完全失配，全反射）
$\begin{vmatrix}\Gamma\end{vmatrix}=1,\rho=\infty,K=0,RL=0dB$
1. 终端短路（ $Z_L=0$ )
  当终端短路时，终端电压入射波与反射波等幅反相；而电流入射波与反射波等幅同相
  电压反射系数 $\Gamma_L=-1$
  没有功率传输
  波腹点和波节点相距 $\lambda/4$
2. 终端开路（ $\Z_L=\infty$ ）
  当终端开路时，终端电流入射波与反射波等幅反相；而电压入射波与反射波等幅同相
  电压反射系数 $\Gamma_{L}=1$
3. 终端接纯电抗负载（ $X_L=jX_L$ )
  因负载不消耗能量，终端仍将产生全反射。入射波与反射波叠加结果，终端既不是波腹也不是波节，但沿线仍呈驻波分布
  电压反射系数 $\displaystyle\Gamma_{L}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=\frac{jX_{L}-Z_{0}}{jX_{L}+Z_{0}} =\left |\Gamma_{\mathrm{L}}\right|e^{j\Phi_L}$
  $\displaystyle\left|\Gamma_{\mathrm{L}}\right|=1,\Phi_{\mathrm{L}}=arctg\frac{2X_{L}Z_{0}}{X_{L}^{2}-Z_{0}^{2}}$
  1. 负载为纯感抗（ $X_L>0$ )
    $\displaystyle X_{L}=Z_{0}tg\frac{2\pi}{\lambda}l_{o}\Rightarrow l_{o}=\frac{\lambda}{2\pi}arct g(\frac{X_{L}}{Z_{0}})$
  2. 负载为纯容抗( $X_L<0$ )
    $\displaystyle l_{o}=\frac{\lambda}{2}+\frac{\lambda}{2\pi}arctg(\frac{X_{L}}{Z_{0}})$
驻波波腹值为入射波的两倍，波节值等于零
沿线同一位置的电压电流之间相位差90°
行驻波状态（部分反射）
特点:信号源入射的电磁波功率一部分被终端负载吸收, 另一部分则被反射, 因此传输线上既有行波又有纯驻波, 构成混合波状态
$0<\left|\Gamma\right|<1,1<\rho<\infty,0<K<1,0<RL<\infty$
端接条件：微波传输线终端接任意复数阻抗负载
$\displaystyle\Gamma_{L}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=\frac{R_{L}\pm jX_{L}-Z_{0}}{R_{L}\pm jX_{L}+Z_{0}}= \begin{vmatrix} \Gamma_{L} \end{vmatrix}e^{\pm j\varphi_L}$
$\displaystyle\left|\Gamma_{L}\right|=\sqrt{\frac{\left(R_{L}-Z_{0}\right)^{2}+X_{L}^{2}}{\left(R_{L}+Z_{0}\right)^{2}+X_{L}^{2}}} \quad\Phi_{L}=\arctan\frac{2X_{L}Z_{0}}{R_{L}^{2}+X_{L}^{2}-Z_{0}^{2}}$

Smith圆图

串联电容：沿等电阻圆逆时针移动（串容阻逆）
串联电感：沿等电阻圆顺时针移动（串感阻顺）
并联电感：沿等电导圆逆时针移动（并感导逆）
并联电容：沿等电导圆顺时针移动（并容导顺）

电阻圆半径越大，R越小
电抗圆半径越大，X越小

顺源逆载，（电抗）上感下容

左波节点，刻度为行波系数K
右波腹点，刻度为驻波比 $\rho$

最外层 $|\Gamma|$ =1,纯电抗,纯驻波

左端点短路,右端点开路

一圈为 $0.5\lambda$ ,半圈为 $0.25\lambda$

第四章微波网络

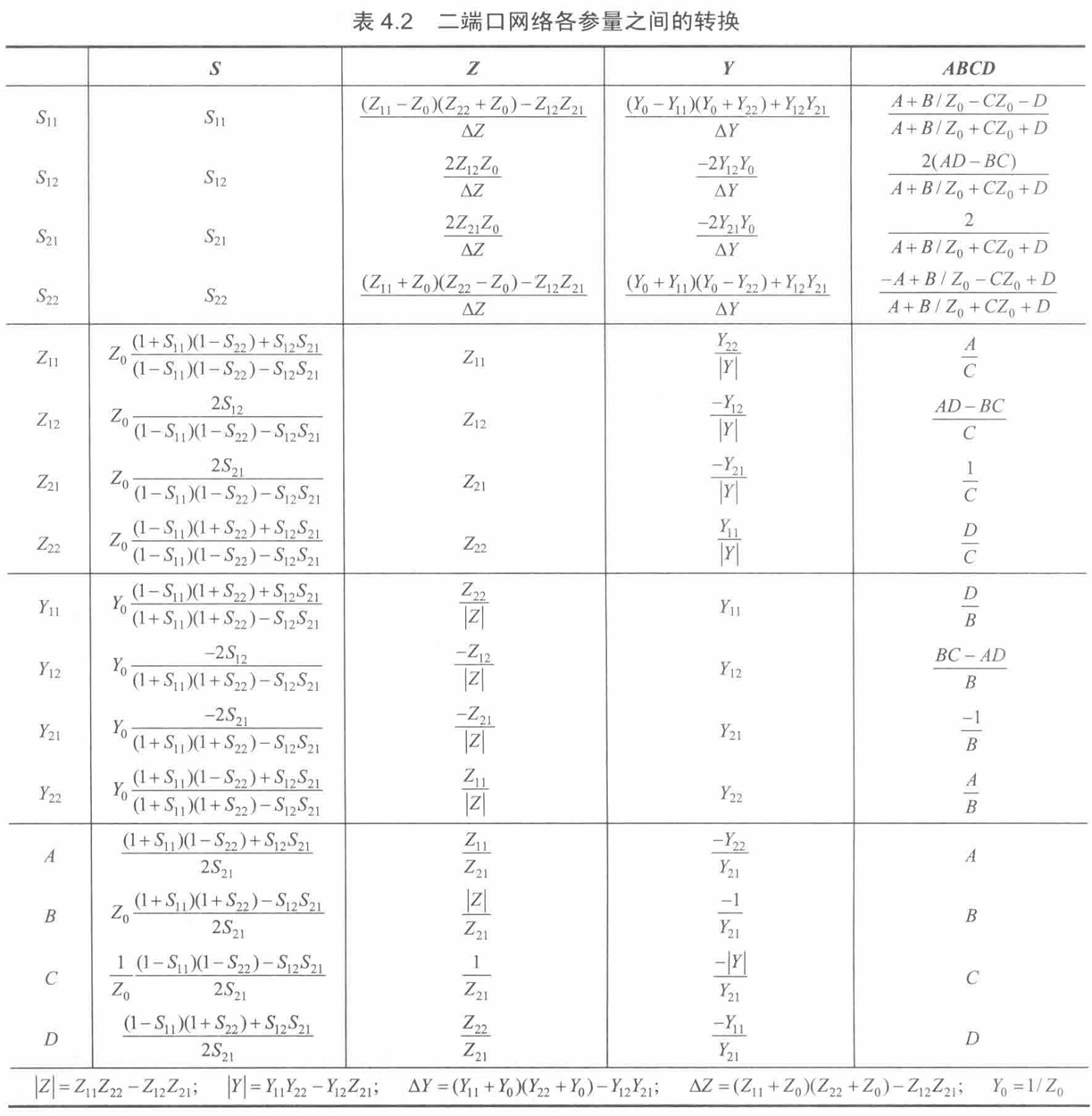
Z矩阵（阻抗矩阵）

$\begin{bmatrix}V_1\\V_2\\\vdots\\V_N\end{bmatrix}=\begin{bmatrix}Z_{11}&Z_{12}&\cdots&Z_{1N}\\Z_{21}&Z_{22}&\cdots&Z_{2N}\\\vdots&\vdots&\ddots&\vdots\\Z_{N1}&Z_{N2}&\cdots&Z_{NN}\end{bmatrix}\begin{bmatrix}I_1\\I_2\\\vdots\\I_N\end{bmatrix}$

$Z_{ii}$ :i口的自阻抗

$Z_{ij}$ :j口对i口的互阻抗

$\displaystyle Z_{ii}=\frac{V_{i}}{I_{i}}|_{I_{k}=0}$ (除i口外其余口均开路)

$\displaystyle Z_{ij}=\frac{V_{i}}{I_{j}}|_{I_{k}=0}$ (除j口外其余口均开路)

归一化电流,电压

$\displaystyle v=\frac{V}{\sqrt{Z_{0}}}\quad i=I\sqrt{Z_0}$

$\displaystyle z_{ii}=\frac{Z_{ii}}{Z_{0i}}\quad z_{ij}=\frac{Z_{ij}}{\sqrt{Z_{0i}Z_{0j}}}$

对称网络: $z_{11}=z_{22}=\cdots=z_{nn}$

互易网络: $z_{ij}=z_{ji}$

无耗网络: $Z_{ij}$ 为纯虚数,ij可相等

Y矩阵(导纳矩阵)

$\begin{bmatrix} I_{1} \\ I_{2} \\ \vdots \\ I_{N} \end{bmatrix}= \begin{bmatrix} Y_{11} & Y_{12} & \cdots & Y_{1N} \\ Y_{21} & Y_{22} & \cdots & Y_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ Y_{N1} & Y_{N2} & \cdots & Y_{NN} \end{bmatrix} \begin{bmatrix} V_{1} \\ V_{2} \\ \vdots \\ V_{N} \end{bmatrix}$

Z,Y矩阵互为逆矩阵

对称网络: $Y_{ii}=Y_{jj}$

互易网络: $Y_{ij}=Y_{ji}$

无耗网络: $Y_{ij}$ 为纯虚数

Z矩阵-串联网络
Y矩阵-并联网络

A矩阵(传输矩阵)

只适用于二端口网络(已知输出求输入)

$\begin{bmatrix} V_{1} \\ I_{1} \end{bmatrix}= \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} V_{2} \\ I_{2} \end{bmatrix}$

$\displaystyle A=\frac{V_{1}}{V_{2}}|_{I_{2}=0}$

归一化后 $\displaystyle a=A\sqrt{\frac{Z_{02}}{Z_{01}}}$

对称矩阵: $a=d$

互易矩阵: $ad-bc=1\Rightarrow|a|=1$

无耗矩阵a,d是实数.b,c为虚数

级联时 $\displaystyle [a]=\prod_{i=1}^{n}[a_{i}]$

常见电路的A矩阵

串联阻抗

$\begin{bmatrix} A & B \\ C & D \end{bmatrix}= \begin{bmatrix} 1 & Z \\ 0 & 1 \end{bmatrix}$
并联导纳

$\begin{bmatrix} A & B \\ C & D \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ Y & 1 \end{bmatrix}$
N：1变压器

$\begin{bmatrix} A & B \\ C & D \end{bmatrix}= \begin{bmatrix} N & 0 \\ 0 & \frac{1}{N} \end{bmatrix}$
传输线

$\begin{bmatrix} A & B \\ C & D \end{bmatrix}= \begin{bmatrix} cos\beta l & jZ_{0}sin\beta l \\ jY_{0}sin\beta l & cos\beta l \end{bmatrix}$

S矩阵(散射矩阵)

$\begin{bmatrix} V_{1}^{-} \\ V_{2}^{-} \\ \vdots \\ V_{N}^{-} \end{bmatrix}= \begin{bmatrix} S_{11} & S_{12} & \cdots & S_{1N} \\ S_{21} & S_{22} & \cdots & S_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ S_{N1} & S_{N2} & \cdots & S_{NN} \end{bmatrix} \begin{bmatrix} V_{1}^{+} \\ V_{2}^{+} \\ \vdots \\ V_{N}^{+} \end{bmatrix}$

$\displaystyle a=\frac{V^{+}e^{-\gamma z}}{\sqrt{Z_{0}}}(\text{入射波})\quad b=\frac{V^{-}e^{\gamma z}}{\sqrt{Z_{0}}}(\text{散射波})$

$\begin{cases} \displaystyle a=\frac{1}{2}(\frac{V}{\sqrt{z_{0}}}+I\sqrt{Z_{0}})=\frac{1}{2}(u+i) \\ \displaystyle b=\frac{1}{2}(\frac{V}{\sqrt{z_{0}}}-I\sqrt{Z_{0}})=\frac{1}{2}(u-i) & \end{cases}\Rightarrow \begin{cases} u=a+b \\ i=a-b & \end{cases}$

$[A]^{\dagger}=([A]^{T})^{\ast}=([A]^{\ast})^{T}$

对称网络: $S_{ii}=S_{jj}(\text{全对称})\quad S_{ik}=S_{jk}(\text{部分对称})$

无耗网络: $[S^{\dagger}][S]=[I]$ ,说明 $[S]$ 是幺正矩阵

证明：

$\begin{aligned} P_{\mathrm{avg}} & =\frac{1}{2}\operatorname{Re}\{V^{t}\boldsymbol{I}^{*}\}=\frac{1}{2}\operatorname{Re}\{(V^{+t}+V^{-t})(V^{+^*}-V^{-^*})\} \\ & =\frac{1}{2}\operatorname{Re}\{V^{+t}V^{+^*}-V^{+t}V^{-^*}+V^{-t}V^{+^*}-V^{-t}V^{-^*}\} \\ & =\frac{1}{2}V^{+t}V^{+^*}-\frac{1}{2}V^{-t}V^{-^*}=0 \end{aligned}$

互易网络: $[S]=[S]^T$

第五章阻抗匹配与调谐

L型网络匹配

解析法：

先串再并

$B=\frac{X_{L}\pm\sqrt{R_{L}/Z_{0}}\sqrt{R_{L}^{2}+X_{L}^{2}-Z_{0}R_{L}}}{R_{L}^{2}+X_{L}^{2}}$

$X=\frac{1}{B}+\frac{X_{L}Z_{0}}{R_{L}}-\frac{Z_{0}}{BR_{L}}$

先并再串

$X=\pm\sqrt{R_{L}(Z_{0}-R_{L})}-X_{L}$

$B=\pm\frac{\sqrt{(Z_0-R_L)/R_L}}{Z_0}$

Smith圆图法

单短截线调谐

1/4波长阻抗变换器

反射系数频率特性：

$|\Gamma|=\frac{1}{\left\{1+[4Z_{0}Z_{L}/(Z_{L}-Z_{0})^{2}]\sec^{2}\theta\right\}^{1/2}},$

假设频率接近于设计频率 $f_{0}$ ,有 $\ell\approx\lambda_0/4$ 和 $\theta\approx\pi/2$ 。于是 $\sec^2\theta\gg1$

$\left|\Gamma\right|\approx\frac{\left|Z_L-Z_0\right|}{2\sqrt{Z_0Z_L}}\left|\cos\theta\right|,\theta\text{接近于}\pi/2$

相对带宽

$\frac{\Delta f}{f_0}=\frac{2(f_0-f_m)}{f_0}=2-\frac{4}{\pi}\arccos\left[\frac{\Gamma_m}{\sqrt{1-\Gamma_m^2}}\frac{2\sqrt{Z_0Z_L}}{\left|Z_L-Z_0\right|}\right]$

当 $Z_L$ 变得接近 $Z_0$ 时(小失配负载),变换器的带宽增加

小反射理论

证明:

局部反射和传播系数

$\begin{aligned}&\Gamma_{1}=\frac{Z_2-Z_1}{Z_2+Z_1}\\&\Gamma_{2}=-\Gamma_{1}\\&\Gamma_3=\frac{Z_L-Z_2}{Z_L+Z_2}\\&T_{21}=1+\Gamma_{1}=\frac{2Z_{2}}{Z_{1}+Z_{2}}\\&T_{12}=1+\Gamma_{2}=\frac{2Z_{1}}{Z_{1}+Z_{2}}\end{aligned}$

总反射系数

$\Gamma=\Gamma_1+T_{12}T_{21}\Gamma_3\mathrm{e}^{-2\mathrm{j}\theta}+T_{12}T_{21}\Gamma_3^2\Gamma_2\mathrm{e}^{-4\mathrm{j}\theta}+\cdots=\Gamma_1+T_{12}T_{21}\Gamma_3\mathrm{e}^{-2\mathrm{j}\theta}\sum_{n=0}^\infty\Gamma_2^n\Gamma_3^n\mathrm{e}^{-2\mathrm{j}n\theta}$

求和,得到

$\begin{aligned} \Gamma & =\Gamma_{1}+\frac{T_{12}T_{21}\Gamma_3e^{-2j\theta}}{1-\Gamma_2\Gamma_3e^{-2j\theta}} \\ & =\frac{\Gamma_1+\Gamma_3e^{-2j\theta}}{1+\Gamma_1\Gamma_3e^{-2j\theta}}\boldsymbol{\approx}\Gamma_{1}+\Gamma_{3}e^{-2j\theta} \end{aligned}$

第六章微波谐振器

串联和并联谐振器

传输线谐振器

短路** $\lambda/2$ 传输线(串联谐振)**

$Z_{\mathrm{in}}=Z_{0}\frac{\tanh\alpha\ell+\mathrm{j}\tan\beta\ell}{1+\mathrm{j}\tan\beta\ell\tanh\alpha\ell}$

考虑在谐振频率附近: $\omega=\omega_{0}+\Delta\omega$

考虑低损耗: $\alpha\ell\ll1\rightarrow\tanh\alpha\ell\approx\alpha\ell$

考虑TEM模: $\beta\ell=\frac{\omega\ell}{v_{p}}=\frac{\omega_{0}\ell}{v_{p}}+\frac{\Delta\omega\ell}{v_{p}}$

考虑 $\lambda/2$ （中心频率处）传输线: $\tan\beta\ell=\tan\left(\pi+\frac{\Delta\omega\pi}{\omega_{0}}\right)=\tan\frac{\Delta\omega\pi}{\omega_{0}}\approx\frac{\Delta\omega\pi}{\omega_{0}}$

由此得出

$Z_{\mathrm{in}}\approx Z_{0}\frac{\alpha\ell+\mathrm{j}(\Delta\omega\pi/\omega_{0})}{1+\mathrm{j}(\Delta\omega\pi/\omega_{0})\alpha\ell} \approx Z_{0}\left(\alpha\ell+\mathrm{j}\frac{\Delta\omega\pi}{\omega_{0}}\right)$

等效串联LC谐振电路参数

$R=Z_{0}\alpha\ell\quad L=\frac{Z_{0}\pi}{2\omega_{0}}\quad C=\frac{1}{\omega_0^2L}\quad Q=\frac{\omega_{0}L}{R}=\frac{\pi}{2\alpha\ell}=\frac{\beta}{2\alpha}$

短路** $\lambda/4$ 传输线(并联谐振)**

$Z_{in}=Z_{0}\mathrm{tanh}(\alpha+\mathrm{j}\beta)\ell=Z_{0}\frac{1-\mathrm{j}\tanh\alpha\ell\cot\beta\ell}{\tanh\alpha\ell-\mathrm{j}\cot\beta\ell}$

考虑 $\lambda/4$ （中心频率处）传输线: $\cot\beta\ell=\cot\left(\frac{\pi}{2}+\frac{\pi\Delta\omega}{2\omega_{0}}\right)=-\tan\frac{\pi\Delta\omega}{2\omega_{0}}\approx\frac{-\pi\Delta\omega}{2\omega_{0}}$

由此得出

$Z_{\mathrm{in}}=Z_{0}\frac{1+\mathrm{j}\alpha\ell\pi\Delta\omega/2\omega_{0}}{\alpha\ell+\mathrm{j}\pi\Delta\omega/2\omega_{0}}\approx\frac{Z_{0}}{\alpha\ell+\mathrm{j}\pi\Delta\omega/2\omega_{0}}$

等效并联谐振电路参数

$R=\frac{Z_0}{\alpha\ell}\quad L=\frac{1}{\omega_{0}^{2}C}\quad C=\frac{\pi}{4\omega_{0}Z_{0}}\quad Q=\omega_{0}RC=\frac{\pi}{4\alpha\ell}=\frac{\beta}{2\alpha}$

开路** $\lambda/2$ 传输线(并联谐振)**

$Z_{\mathrm{in}}=Z_{0}\coth(\alpha+\mathrm{j}\beta)\ell=Z_{0}\frac{1+\mathrm{j}\tan\beta\ell\tanh\alpha\ell}{\tanh\alpha\ell+\mathrm{j}\tan\beta\ell}$

$Z_{\mathrm{in}}\approx\frac{Z_{0}}{\alpha\ell+\mathbf{j}(\Delta\omega\pi/\omega_{0})}$

等效并联谐振参数

$R=\frac{Z_{0}}{\alpha\ell}\quad L=\frac{1}{\omega_{0}^{2}C}\quad C=\frac{\pi}{2\omega_{0}Z_{0}} \quad Q=\omega_{0}RC=\frac{\pi}{2\alpha\ell}=\frac{\beta}{2\alpha}$

矩形波导谐振腔

波导谐振波数

$k_{mn\ell}=\sqrt{\left(\frac{m\pi}{a}\right)^{2}+\left(\frac{n\pi}{b}\right)^{2}+\left(\frac{\ell\pi}{d}\right)^{2}}$

谐振频率

$f_{mn\ell}=\frac{ck_{mn\ell}}{2\pi\sqrt{\mu_{r}\epsilon_{1}}}=\frac{c}{2\pi\sqrt{\mu_{r}\epsilon_{r}}}\sqrt{\left(\frac{m\pi}{a}\right)^{2}+\left(\frac{n\pi}{b}\right)^{2}+\left(\frac{\ell\pi}{d}\right)^{2}}$

临界耦合

在谐振频率处,谐振器与传输线匹配,能实现谐振腔与传输线的最大功率传输,称为谐振腔临界耦合到传输线

耦合系数 $\displaystyle g=\frac{\text{无载}Q_{0}}{\text{外部}Q_{e}}$

g<1:此时称谐振器欠耦合到馈线
g=1:此时称谐振器临界耦合到馈线
g>1:此时称谐振器过耦合到馈线

第七章功率分配器和定向耦合器

功率分配器

互易、无耗、三端口匹配不能同时实现

证明：

放宽互易条件
匹配时

$[S]= \begin{bmatrix} 0 & S_{12} & S_{13} \\ S_{21} & 0 & S_{23} \\ S_{31} & S_{32} & 0 \end{bmatrix}$

根据无耗条件 $[S][S]^{\dagger}=I$ ,得到

$|S_{12}|^{2}+|S_{13}|^{2}=1\\ |S_{21}|^{2}+|S_{23}|^{2}=1\\ |S_{31}|^{2}+|S_{32} |^{2}=1$

$S_{13}^{*}S_{23}=0\\ S_{23}^{*}S_{12}=0\\ S_{12}^{*}S_{13}=0$

矛盾,无法互易

定向耦合器

任意互易、无耗、匹配的四端口网络是一个定向耦合器

耦合度C

输入端的输入功率P1，与耦合端的输出功率P3之比的分贝数

$\mathrm{C}=10\lg\frac{P_1}{P_3}=20\lg\frac{\left|a_1\right|^2}{\left|b_3\right|^2}=20\lg\frac{1}{\left|S_{31}\right|}=20\lg\frac{1}{\left|S_{13}\right|}$

隔离度I

输入端的输入功率P1，与隔离端的输出功率P4之比的分贝数

$\mathrm{I}=10\lg\frac{P_{1}}{P_{4}}=10\lg\frac{\left|a_{1}\right|^{2}}{\left|b_{4}\right|^{2}} =20\lg\frac{1}{\left|S_{41}\right|}=20\lg\frac{1}{\left|S_{14}\right|}$

方向性D

耦合端输出功率P3与隔离端的输出功率P4之比的分贝数

$\mathrm{D}=10\lg\frac{P_{3}}{P_{4}}=20\lg\frac{\left|\mathrm{b}_{3}\right|^{2}}{\left|b_{4}\right|^{2}} =I-C$

输入驻波比ρ

定向耦合器除输入端外，其余各端均接上匹配负载时，输入端的驻波比即为定向耦合器的输入驻波比

$\rho=\frac{1+|S_{11}|}{1-|S_{11}|}$

频带宽度

频带宽度是指耦合度、隔离度(或方向性)及输入驻波比都满足指标要求时，定向耦合器的工作频带宽度。简称工作带宽

Wilikinson功率分配器

特点:

三个端口同时匹配，而且两个输出端口隔离，有耗
通常制成带状线或微带线的形式
当输出端口都匹配的时候，对输入波仍具有无耗的特性
与T形接头结构相比较其最大变化是在两分支臂距分支点λ/4处跨接一个阻值为R的电阻，用以实现端口2和端口3的隔离

$\frac{P_2}{P_3}=\frac{Z_{in3}}{Z_{in2}}=\frac{R_2}{Z_{02}^2}\cdot\frac{Z_{03}^2}{R_3}=\frac{1}{k^2}$

$Y_0=\frac{1}{Z_0}=\frac{R_2}{Z_{02}^2}+\frac{R_3}{Z_{03}^2}$

由上述两式解得：

$Z_{02}=Z_0\sqrt{k\left(1+k^2\right)}$

$Z_{03}=Z_{0}\sqrt{\frac{1+k^{2}}{k^{3}}}$

$R=\frac{1+k^{2}}{k}Z_{0}(\text{隔离电阻})$

3dB功率分配器(k=1)

$[S]= \begin{bmatrix} 0 & -j\frac{1}{\sqrt{2}} & -j\frac{1}{\sqrt{2}} \\ \\ -j\frac{1}{\sqrt{2}} & 0 & 0 \\ \\ -j\frac{1}{\sqrt{2}} & 0 & 0 \end{bmatrix}$

此时$Z_{02}=\sqrt{2}Z_{0} \quad Z_{03}=\sqrt{2}Z_{0} \quad R_{2}=kZ_0=Z_{0} \quad R_{3}=\frac{Z_0}{k}=Z_{0} \quad R=2Z_{0} $

正交混合网络

特点:直通和耦合臂的输出有90度相位差；正交混合网络是分支定向耦合器特例，是3dB定向耦合器；通常为微带或带状线形式；分支线定向耦合器有高度的对称性,任何一个端口都可以作为输入端口

$[S]=\frac{-1}{\sqrt{2}} \begin{bmatrix} 0 & \mathrm{j} & 1 & 0 \\ \mathrm{j} & 0 & 0 & 1 \\ 1 & 0 & 0 & \mathrm{j} \\ 0 & 1 & \mathrm{j} & 0 \end{bmatrix}$

奇模和偶模等效电路的ABCD矩阵

$A_o=\begin{bmatrix}1&0\\\\-ja_1Y_{01}&1\end{bmatrix}\cdot\begin{bmatrix}0&\frac{j}{bY_{01}}\\\\jbY_{01}&0\end{bmatrix}\cdot\begin{bmatrix}1&0\\\\-ja_2Y_{01}&1\end{bmatrix}=\begin{bmatrix}\frac{a_2}{b}&\frac{j}{bY_{01}}\\j(\mathbf{b}-\frac{a_1a_2}{b})Y_{01}&\frac{a_1}{b}\end{bmatrix}$

$\begin{gathered}A_e=\begin{bmatrix}1&0\\ja_1Y_{01}&1\end{bmatrix}\cdot\begin{bmatrix}0&\frac{j}{bY_{01}}\\jbY_{01}&0\end{bmatrix}\cdot\begin{bmatrix}1&0\\ja_2Y_{01}&1\end{bmatrix}=\begin{bmatrix}-\frac{a_2}{b}&\frac{j}{bY_{01}}\\j(\mathrm{b-}\frac{a_1a_2}{b})Y_{01}&-\frac{a_1}{b}\end{bmatrix}\end{gathered}$

奇模和偶模等效电路的归一化ABCD矩阵

$\overline{A}_e=\begin{bmatrix}-\frac{a_2}{b}\sqrt{R}&\frac{j}{b\sqrt{R}}\\j(\mathrm{b}-\frac{a_1a_2}{b})\sqrt{R}&-\frac{a_1}{b\sqrt{R}}\end{bmatrix}$

$\overline{A}_o=\begin{bmatrix}\frac{a_2}{b}\sqrt{R}&\frac{j}{b\sqrt{R}}\\j(\mathrm{b}-\frac{a_1a_2}{b})\sqrt{R}&\frac{a_1}{b\sqrt{R}}\end{bmatrix}$

$\sqrt{R}=\sqrt{Y_{01}/Y_{02}}$

耦合线定向耦合器

$\begin{gathered} [S]= \begin{bmatrix} 0 & -j\sqrt{1-k^{2}} & k & 0 \\ -j\sqrt{1-k^{2}} & 0 & 0 & k \\ k & 0 & 0 & -j\sqrt{1-k^{2}} \\ 0 & k & -j\sqrt{1-k^{2}} & 0 \end{bmatrix} \end{gathered}$

第八章微波滤波器

设计原型低通滤波器

$P_{\mathrm{LR}}=\frac{\text{来自源的可用功率}}{\text{传送到负载的功率}}=\frac{P_{\mathrm{inc}}}{P_{\mathrm{lond}}}=\frac{1}{1-|\Gamma(\omega)|^{2}}$

最平坦（二项式或巴特沃兹）滤波器响应

$P_{\mathrm{LR}}=1+k^{2}\left(\frac{\omega}{\omega_{c}}\right)^{2N}$

等纹波滤波器响应

$P_{\mathrm{LR}}=1+k^{2}T_{N}^{2}\left(\frac{\omega}{\omega_{c}}\right)$

滤波器阻抗和频率定标

低通滤波器定标

$L_{k}^{\prime}=\frac{R_{0}L_{k}}{\omega_{c}}\quad C_{k}^{\prime}=\frac{C_{k}}{R_{0}\omega_{c}}$

低通到高通的变换

$C_{k}^{\prime}=\frac{1}{R_{0}\omega_{c}L_{k}}\quad L_{k}^{\prime}=\frac{R_{0}}{\omega_{c}C_{k}}$

低通到带通的变换

相对带宽 $\displaystyle\Delta=\left(\frac{\omega_{2}-\omega_{1}}{\omega_{0}}\right)$

串联电感转换成电感和电容串联

$L_{k}^{\prime}=\frac{L_{k}R_{0}}{\omega_{0}\Delta}\quad C_{k}^{\prime}=\frac{\Delta}{\omega_{0}L_{k}R_{0}}$

并联电容转换成LC并联电路

$L_{k}^{\prime}=\frac{\Delta R_{0}}{\omega_{0}C_k}\quad C_{k}^{\prime}=\frac{C_k}{\omega_{0}\Delta R_{0}}$

低通到带阻的变换

串联电感转换为LC并联电路

$L_{k}^{\prime}=\frac{\Delta L_{k}R_0}{\omega_{0}} \quad C_{k}^{\prime}=\frac{1}{\omega_{0}\Delta L_{k}R_0}$

并联电容转换为LC串联电路

$L_{k}^{\prime}=\frac{R_0}{\omega_{0}\Delta C_{k}}\quad C_{k}^{\prime}=\frac{\Delta C_{k}}{\omega_{0}R_0}$

滤波器实现

理查德变换

$\Omega=\tan\beta\ell=\tan\left(\frac{\omega\ell}{v_{p}}\right)$

电感变成短路短截线

电感的电抗 $\mathrm{j}X_L=\mathrm{j}\Omega L=\mathrm{j}L\tan\beta\ell$

电感可以用特性阻抗为L，电长度为βl的短路线段等效

电容变成开路短截线

电容的电纳 $\mathrm{j}B_{C}=\mathrm{j}\Omega C=\mathrm{j}C\tan\beta\ell$

电容可以用特性阻抗为1/C，电长度为βl的开路线段等效

对于原型低通滤波器：截止频率Ω为1，对应的线段的长度为λ/8

集总参数元件设计的滤波器中的电容和电感都可以用开路或短路线等效，而且这些线长度相等，称为为公比线

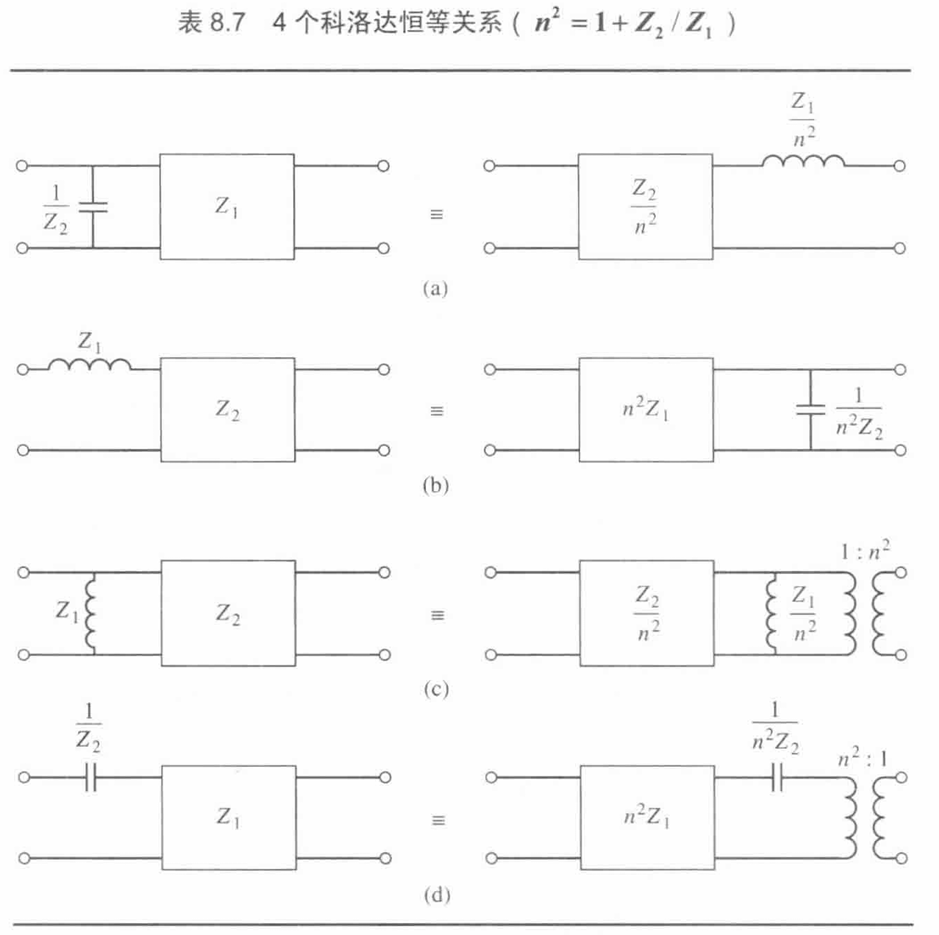
科洛达恒等关系

第二章 传输线理论

第四章 微波网络

第五章 阻抗匹配与调谐

第六章 微波谐振器

第七章 功率分配器和定向耦合器

第八章 微波滤波器